答案:C
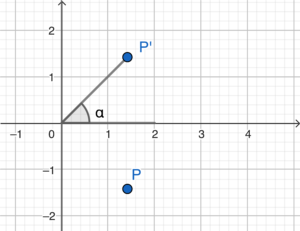
將 $P$ 經變換後的像記為 $P’$。

留意 $P’$ 的直角坐標為 $(\sqrt{2},\sqrt{2})$。
$\begin{array}{cl}
& OP’ \\
= & \sqrt{(\sqrt{2})^2 +(\sqrt{2})^2} \\
= & 2
\end{array}$
另外,
$\begin{array}{rcl}
\tan \alpha & = & \dfrac{\sqrt{2}}{\sqrt{2}} \\
\tan \alpha & = & 1 \\
\alpha & = & 45^\circ
\end{array}$
所以,$P’$ 的極坐標為 $(2, 45^\circ)$。

