答案:C
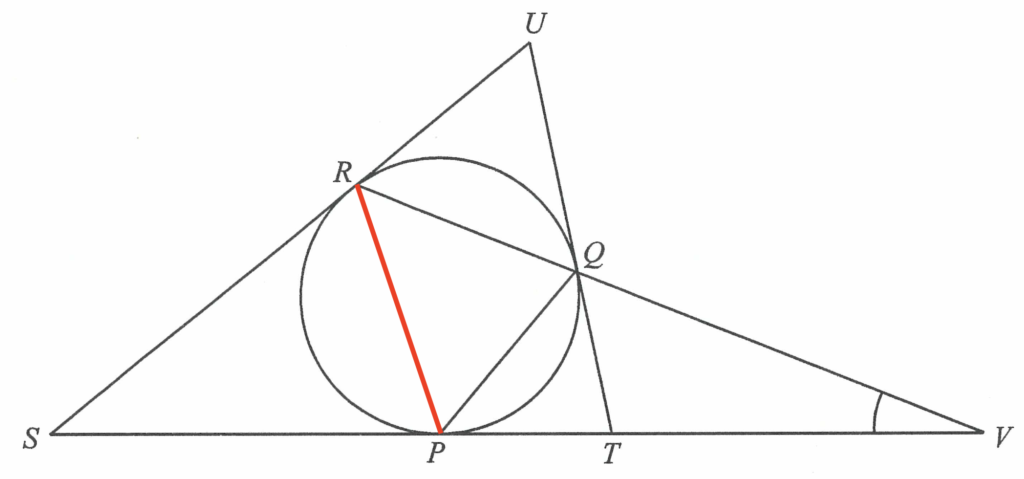
連結 $P$ 及 $R$。

由於 $SU$ 及 $ST$ 分別為圓於 $R$ 及 $P$ 的切線,可得
$\begin{array}{rcll}
SR & = & SP & \text{(切線性質)} \\
\therefore \angle SRP & = & \angle SPR & \text{(等腰三角形的底角)} \\
\angle SRP & = & \dfrac{1}{2} (180^\circ -\angle PSR) & \text{(三角形的內角和)} \\
\angle SRP & = & \dfrac{1}{2}(180^\circ-34^\circ) \\
\angle SRP & = & 73^\circ
\end{array}$
另外,
$\begin{array}{rcll}
\angle PRQ & = & \angle QPT & \text{(內錯弓形的圓周角)} \\
\angle PRQ & = & 46^\circ
\end{array}$
在 $\Delta RSV$,可得
$\begin{array}{rcll}
\angle PVQ & = & 180^\circ -\angle RSV-\angle SRP-\angle PRV & \text{(三角形的內角和)} \\
\angle PRV & = & 180^\circ-34^\circ-73^\circ-46^\circ \\
\angle PRV & = & 27^\circ
\end{array}$

