答案:C
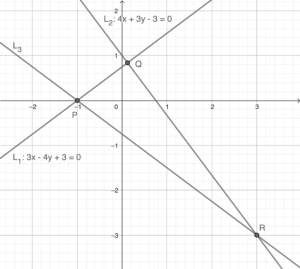
依題意略繪下圖。在以下略圖中,假定 $k=3$。

留意 $\Delta PQR$ 的內心在 $x$ 軸之上。所以 $x$ 軸為 $\angle QPR$ 的角平分線。由此,$PQ$ 為把 $L_1$ 對 $x$ 軸反射的像。
$L_1$ 的方程為
$\begin{array}{rcl}
3x-4y+k & = & 0 \\
4y & = & 3x+k \\
y & = & \dfrac{3x+k}{4}
\end{array}$
所以,$PR$ 的方程為
$\begin{array}{rcl}
y & = & -\left(\dfrac{3x+k}{4}\right) \\
y & = & \dfrac{-3x-k}{4}
\end{array}$
對於 $R$ 的坐標,
$\left\{ \begin{array}{ll}
4x+3y-k=0 & \ldots \unicode{x2460} \\
y=\dfrac{-3x-k}{4} & \ldots \unicode{x2461}
\end{array}\right.$
把 $\unicode{x2461}$ 代入 $\unicode{x2460}$,可得
$\begin{array}{rcl}
4x+3\left(\dfrac{-3x-k}{4}\right)-k & = & 0 \\
4x+\dfrac{-9x-3k}{4}-k & = & 0 \\
16x -9x-3k-4k & = & 0 \\
7x & = & 7k \\
x & = & k
\end{array}$

