2023-II-19
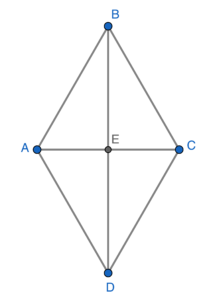
I 不一定正確。根據菱形的定義,$AB=BC=CD=DA$。參考上圖,可以清楚看到 $AE\ne

I 不一定正確。根據菱形的定義,$AB=BC=CD=DA$。參考上圖,可以清楚看到 $AE\ne
由於 $ABCD$ 為一正方形,$\angle BAD=90^\circ$。
由於 $ADEFG$ 為一
A 為不正確。考慮 $\Delta RTV$。已知 $RT=RV$,則 $\angle RTV = \ang
設 $\angle TSU =x$。在 $\Delta STU$ 中,可得
$\begin{array}{
在 $\Delta ABE$ 中,
$\begin{array}{rcll}
\angle AEB �
將 $P$ 經變換後的像記為 $P’$。
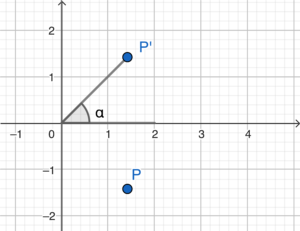
留意 $P’$ 的直角坐標為 $(\sq
留意直線 $2x+(a+3)y-5=0$ 的斜率為 $\dfrac{-2}{a+3}$。
也留意直線
I 正確。留意 $\ell$ 及 $L$ 的斜率相等。由此,$\Gamma$ 為一與 $\ell$ 及 $L$
I 不正確。留意 $G_1$ 及 $G_2$ 的坐標分別為 $\left(\dfrac{-7}{2},2
下表為樣本空間。
$\begin{array}{|c|c|c|c|c|c|} \hline
�
留意該分佈的上四分位數為中間的「箱」的最右方的數值,即 $60$。
平均薪金
$\begin{array}{cl}
= & \dfrac{14\times 31
$\begin{array}{cl}
& 1011001011001011_2 \\
= &
在該三個數式中,$a$、$b$ 及 $c$ 的最高次數分別為 $4$、$5$ 及 $2$。所以,該 L.C
利用直線方程的截距式,可得
$\begin{array}{rcl}
\dfrac{\log_4 x
$\begin{array}{cl}
& \dfrac{i}{k-i}+\dfrac{
把原圖像函數的方程改寫為頂點式,可得
$\begin{array}{rcl}
f(x) &
設 $a$ 及 $d$ 分別為該等差數列的首項與公差。
$\begin{array}{rcl}
T(11
考慮聯立方程組
$\left\{ \begin{array}{ll}
x+3=0 & \ld
連結 $P$ 及 $R$。
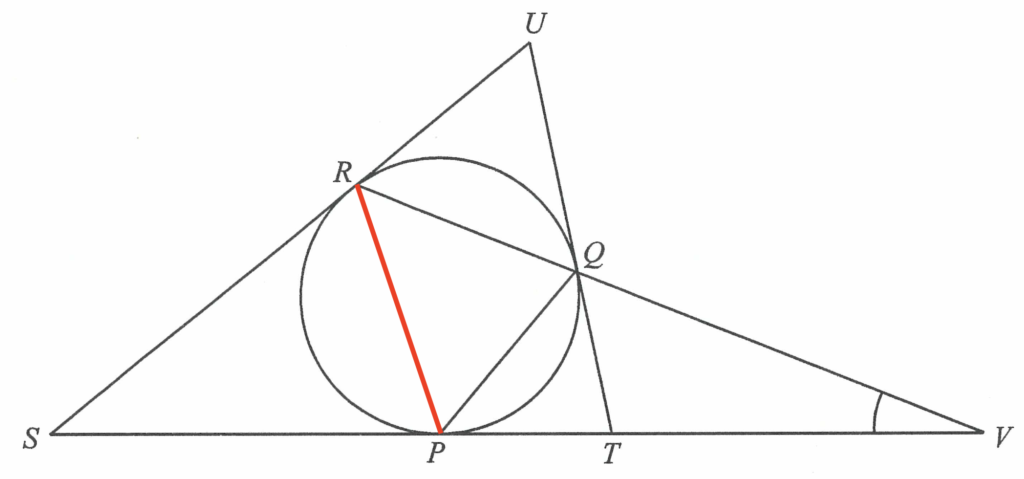
由於 $SU$ 及 $ST$ 分別為圓於 $R$ 及 $P$ 的切線,可得
$\begin
