香港中學文憑-數學 - 2015

答案：D
$\begin{array}{cl}
& \dfrac{(3y^6)^4}{3y^2}

答案：A
$\left\{ \begin{array}{ll}
p+3q = 4 & \ldots \un

答案：D
$\begin{array}{cl}
& 0.002\ 345\ 678\ 9 \\
= 

答案：B
$\begin{array}{rcl}
x^2 + mx + n & \equiv & (

答案：A
$\begin{array}{rcl}
18 + 7x & & 4 \\
7x &

答案：A
由於 $\beta$ 為方程 $4x^2 -5x – 1=0$ 的一個解，則可得

$\begin

答案：D
由於圖像的開口向上，所以 $a0$。

留意圖像的 $x$ 截距在負 $x$ 軸之上，所以其根必為負數。考

答案：B
設 $\$x$ 為該紀念品的售價。則新的售價

$\begin{array}{cl}
= & x

答案：D
所求的本利和

$\begin{array}{cl}
= & 50\ 000 \times (1 +

答案：C
$\begin{array}{ccccccccccc}
a & : & &

答案：D
設 $z = kx^3y^2$，其中 $k$ 為非零常數。把 $x=2$、$y=1$ 及 $z=14$ 代入 $

答案：B
留意 $T(1)=5$ 及對於任意正整數 $n$，$T(n+1) = T(n) + 4$。

$\begin{

答案：C
留意該袋白砂糖的最大可取重量為 $5.5\text{ kg}$，且一包白砂糖的最小可取重量為 $9

答案：C
在 $\Delta CDN$ 運用畢氏定理，可得

$\begin{array}{rcl}
CD^2 &#

答案：B

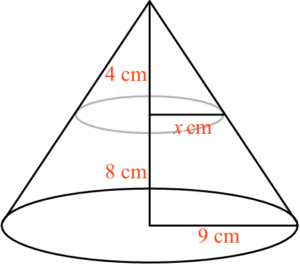
設 $x\text{ cm}$ 為該平截頭體上底的半徑。由此，可得

$\begin{array}{r

答案：D
留意 $ABCD$ 為一平行四邊形，則 $AD//BC$。

由此，$AF// BG$。

考慮 $\Delt

答案：A
考慮 $\Delta ABC$，可得

$\begin{array}{rcl}
\tan \beta &#

答案：C
$\begin{array}{cl}
& \dfrac{\cos 180^\circ}{

答案：C

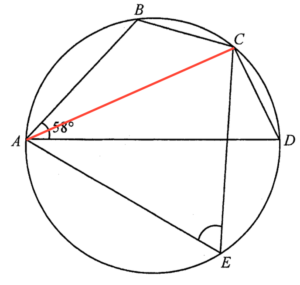
連結 $AC$。

$\begin{array}{ll}
BC = CD & \text{(已知)

答案：B

由於 $AC$ 及 $BD$ 均為圓的直徑，則相交點 $E$ 必定為圓心。所以 $AE$、$EC$、$BE