2021-II-21
I 為正確。
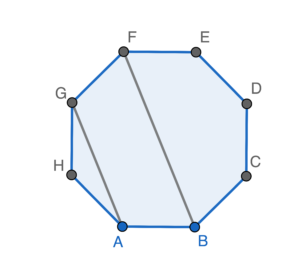
$\begin{array}{rcl}
\angle ABC & = &
I 為正確。

$\begin{array}{rcl}
\angle ABC & = &
$\begin{array}{rcll}
\angle ACD & = & 180^
$P(7,-5)$ 對 $y$ 軸反射至 $Q$,則 $Q=(-7,-5)$。
$Q(-7,-5)$ 繞原
在 $\Delta ACD$ 中,
$\begin{array}{rcll}
\tan \theta &#
設 $(x,y)$ 為 $P$ 的坐標。則 $P$ 的軌跡的方程為
$\begin{array}{rcl}
由於 $AP$ 為 $\Delta ABC$ 的中線,則 $P$ 為 $BC$ 的中點。$P$ 的坐標
$\beg
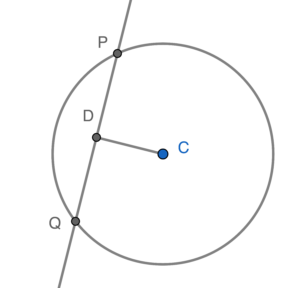
設 $C$ 為圓心。則 $C$ 的坐標
$\begin{array}{cl}
= & \left(
留意該分佈有 $24$ 名工人。則該分佈的下四分位數
$\begin{array}{cl}
= �
四分位數間距
$\begin{array}{cl}
= & 36 -26 \\
= & 1
設 $\mu$ 為餘下 $40$ 個整數的平均值。
$\begin{array}{rcl}
\dfrac
$\begin{array}{rcl}
\text{第 $1$ 個數式} & = &
$\begin{array}{cl}
& 14\times 16^{15} +17 \tim
把 $y=0$ 代入 $y=a+\log_b x$,可得
$\begin{array}{rcl}
0 &#
考慮圖像中直線的方程,可得
$\begin{array}{rcl}
\dfrac{\log_5 y
I 必為正確。對於任何實數 $\alpha$,
$\begin{array}{cl}
& u
I 必為正確。由於 $p$、$q$、$r$ 及 $s$ 為一等比數列,則可得
$\begin{array
對於任何實數 $x$,$x^2+kx+k+8\ge 0$。可得
$\begin{array}{rc
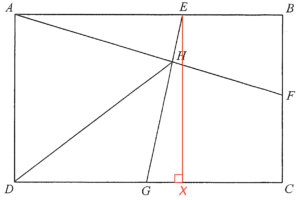
在 $CD$ 上加點 $X$ 使得 $EX \perp CD$。由此 $EX=BC= 597\text{ cm}
連結 $AD$。
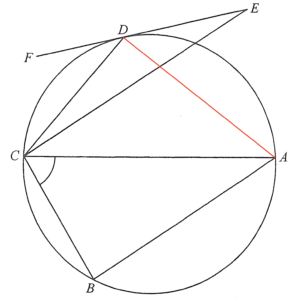
在 $\Delta CDE$ 中,
$\begin{array}{rcll}
\angl
$\left\{ \begin{array}{l}
x^2 +y^2 -4x -22y +75 = 0 �
