香港中學文憑-數學 - 2022

$\begin{array}{cl}
& \dfrac{81^{2n+3}}{(27^

$\begin{array}{rcl}
(x+3)^2+mx & \equiv &

$\begin{array}{rcl}
(x-c)(x-4c) & = & (3c

$\begin{array}{rcl}
\dfrac{2}{u} + \dfrac{3}{v} &#

留意捨入的方法為下捨入，即不足 $1$ 的數值會被捨去。所以，$345\le x < 346$。

$\left\{ \begin{array}{ll}
3y-5 < 5y +1 & \ldots \unicode{x2460} \\ 5y +1 \le 11 & \ldots \unicode{x2461} \end{array}\right.$

從 $\unicode{x2460}

A 不一定正確。留意 $f(k) = k^2 -k +1$。

$\begin{array}{rcl}
f(-

由於 $g(x)$ 可被 $x+2a$ 整除，可得

$\begin{array}{rcl}
g(-2a)

I 為正確。把該圖像的方程改寫為一般式，可得

$\begin{array}{rcl}
y &

所求的利息

$\begin{array}{cl}
= & 88000 \times \left

由於 $x:y=8:5$，設 $x=8k$ 及 $y=5k$，其中 $k \neq 0$。由此，可得

$\b

設 $u=\dfrac{k\sqrt{v}}{w}$，其中 $k\neq 0$。

I 為正確。

$\be

$\begin{array}{rcl}
T(1) & = & 8 \\
T(2) �

設 $r\text{ cm}$ 為該半球體的半徑。則該圓柱體的底半徑及高分別為 $r\text{ cm

設 $O$ 為該圓的圓心。$A$ 為 $B$ 該弦的兩端點。在 $\Delta ABO$ 中，

$\begin

連結 $PN$。

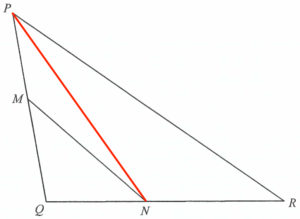
設 $x\text{ cm}^2$ 為 $\Delta MNQ$ 的面積。由於 $\Delt

由於 $ABCD$ 為一長方形，可得

$\begin{array}{rcl}
AB & = &#

在 $\Delta ABD$ 及 $\Delta CAE$ 中，

$\begin{array}{rcll}

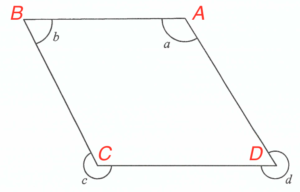
如圖所示，把四個頂點記為 $A$、$B$、$C$ 及 $D$。

I 必為正確。由於 $AD\text{/

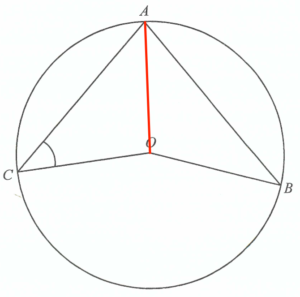
連結 $OA$。

$\begin{array}{rcll}
\angle CAB & = �