香港中學文憑-數學

答案：D

$\left\{ \begin{array}{ll}
\log_4 y = 2x-1 & \ld

答案：A

$\begin{array}{cl}
& 12\text{B}00\text{CD}0

答案：B

$\begin{array}{rcl}
z & = & 4+5i^{10}-ki^

答案：B

$\left\{ \begin{array}{ll}
2x+y = 8 & \ldots \un

答案：D

由於它們為等比數列的項，可得

$\begin{array}{rcl}
\dfrac{a_2}{a

答案：D

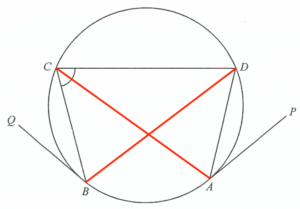
連結 $AC$ 及 $BD$。

$\begin{array}{rcll}
\angle BDC &

答案：C

$\begin{array}{rcl}
\sin^2x & = & 6\cos^2

答案：A

留意 $\alpha = \angle GFH = 45^\circ$。

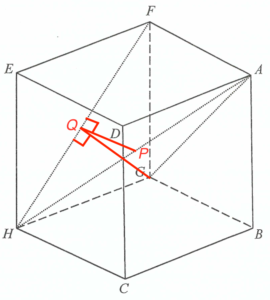
把 $FH$ 及 $AH$ 的中點分別記

答案：A

留意外心的坐標為 $\left(\dfrac{a}{2}, \dfrac{b}{2} \right

答案：B

可組成的密碼數量

$\begin{array}{cl}
= & 5! \times 2! \\
=

答案：B

所求的概率

$\begin{array}{cl}
= & \dfrac{3}{7} \tim

答案：C

新的中位數 $x$

$\begin{array}{cl}
= & 30 \times (1+50

答案：D

I 不正確。$S_1$ 的平均值

$\begin{array}{cl}
= & \dfrac{

答案 $h=\dfrac{15+k^2}{5-k}$

$\begin{array}{rcl}
\dfrac

答案：$x^{34}y^{55}$

$\begin{array}{cl}
& \dfrac{x^

答案：不正確

準確至最接近的 $10\text{ g}$ 的最大絕對誤差

$\begin{array}{cl}

答案：(a) $\dfrac{-9}{2} < x < 3$ (b) $4$

1. 考慮第一條不等式，可得

   $\begin{array}{rcl}

答案：$35$

設 $x$ 及 $y$ 分別為該渡輪上男乘客及女乘客的數目。

$\left\{ \begin{ar

答案：(a) $6:7:17$ (b) $\dfrac{43}{50}$

1. 考慮方程 $7a=6b$，可得

   $\b

答案：$\angle RQS=27^\circ$, $\angle PQS=63^\circ$

在 $\Del