香港中學文憑-數學

由於 $h(x)$ 可被 $2x-3$ 整除，可得

$\begin{array}{rcl}
h\left

A 不正確。把該圖像的方程改寫為一般式，可得

$\begin{array}{rcl}
y &

設 $\$ x$ 為該外套的成本。其標價為

$\begin{array}{cl}
= & x (1

$\begin{array}{cl}
& \text{地圖上的長度} : \text{實際

設 $z=kx^2\sqrt[3]{y}$，其中 $k\neq 0$。

當 $x=12$ 及 $y=64$

$\begin{array}{rcl}
a_8 & = & a_7 +a_6 \\
60

設 $r\text{ cm}$ 及 $h\text{ cm}$ 分別為該直立圓柱體的底半徑及高。

由於該立

將大圓的圓心記為 $O$。

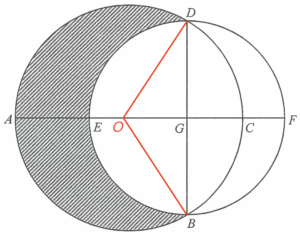
由於 $AC$ 為大圓的一直徑，可得

$\begin{array}{rcl

連結 $R$ 及 $X$。設 $PX:XQ =r:1$，其中 $r0$。

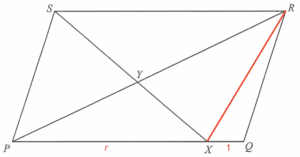
由於 $\Delta PQR$ 及 $\

把各頂點記為 $A$、$B$、$C$、$D$ 及 $E$ 如下圖。

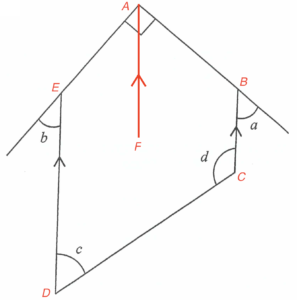
I 必為正確。加點 $F$ 使得 $ED\

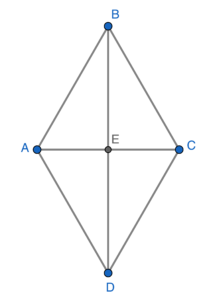
I 不一定正確。根據菱形的定義，$AB=BC=CD=DA$。參考上圖，可以清楚看到 $AE\ne

由於 $ABCD$ 為一正方形，$\angle BAD=90^\circ$。

由於 $ADEFG$ 為一

A 為不正確。考慮 $\Delta RTV$。已知 $RT=RV$，則 $\angle RTV = \ang

設 $\angle TSU =x$。在 $\Delta STU$ 中，可得

$\begin{array}{

在 $\Delta ABE$ 中，

$\begin{array}{rcll}
\angle AEB �

將 $P$ 經變換後的像記為 $P’$。

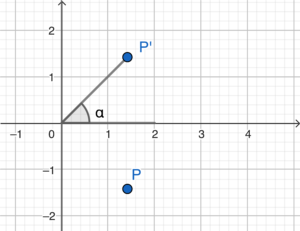
留意 $P’$ 的直角坐標為 $(\sq

留意直線 $2x+(a+3)y-5=0$ 的斜率為 $\dfrac{-2}{a+3}$。

也留意直線

I 正確。留意 $\ell$ 及 $L$ 的斜率相等。由此，$\Gamma$ 為一與 $\ell$ 及 $L$

I 不正確。留意 $G_1$ 及 $G_2$ 的坐標分別為 $\left(\dfrac{-7}{2},2

下表為樣本空間。

$\begin{array}{|c|c|c|c|c|c|} \hline
�