香港中學文憑-數學

留意該分佈的上四分位數為中間的「箱」的最右方的數值，即 $60$。

平均薪金

$\begin{array}{cl}
= & \dfrac{14\times 31

$\begin{array}{cl}
& 1011001011001011_2 \\
= &

在該三個數式中，$a$、$b$ 及 $c$ 的最高次數分別為 $4$、$5$ 及 $2$。所以，該 L.C

利用直線方程的截距式，可得

$\begin{array}{rcl}
\dfrac{\log_4 x

$\begin{array}{cl}
& \dfrac{i}{k-i}+\dfrac{

把原圖像函數的方程改寫為頂點式，可得

$\begin{array}{rcl}
f(x) &

設 $a$ 及 $d$ 分別為該等差數列的首項與公差。

$\begin{array}{rcl}
T(11

考慮聯立方程組

$\left\{ \begin{array}{ll}
x+3=0 & \ld

連結 $P$ 及 $R$。

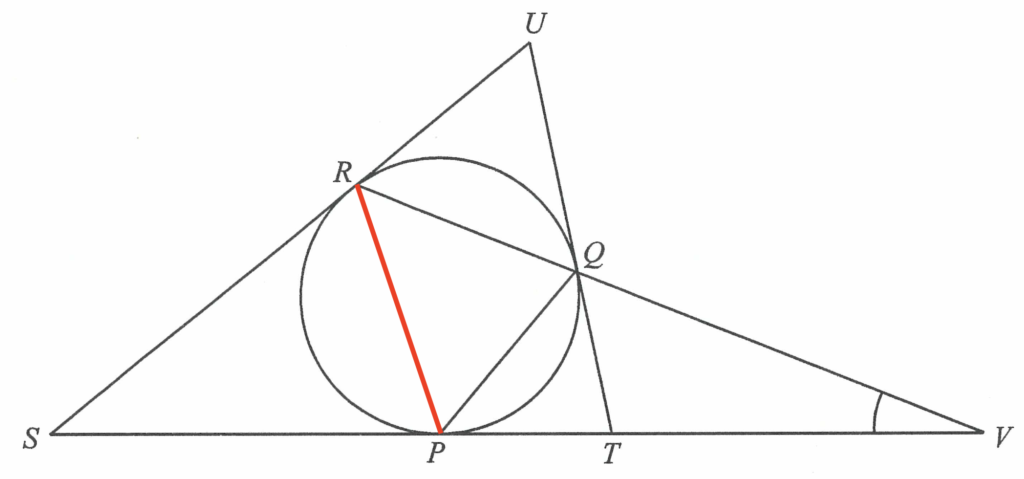
由於 $SU$ 及 $ST$ 分別為圓於 $R$ 及 $P$ 的切線，可得

$\begin

留意 $(1,0)$ 在 $hx+ky=6$ 之上，可得

$\begin{array}{rcl}
h(1

在 $VB$ 上加點 $X$ 使得 $AX\perp VB$ 及 $CX\perp VB$。$\Delta VA

依題意略繪下圖。在以下略圖中，假定 $k=3$。

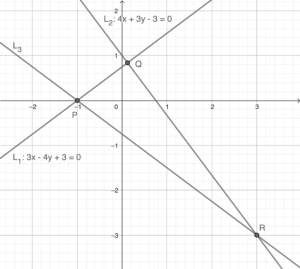
留意 $\Delta PQR$ 的內心在 $x$ 軸之上

所求的數目

$\begin{array}{cl}
= & C^{15}_1 \times C^

所求的概率

$\begin{array}{cl}
= & C^4_2 (0.6)^2(1-0

設 $\mu$ 及 $\sigma$ 分別為該分佈的平均值及標準差。

$\left\{ \begin{a

I 必為正確。若對於 $\{1-9n, 3-9n, 4-9n, 5-9n, 7-9n\}$ 內每個數據加上