香港中學會考 - 2009 - 卷二

答案：D
$\begin{array}{rcl}
2AB & = & 3 BC \\
\dfrac

答案：B
考慮 $\Delta ACD$，

$\begin{array}{rcl}
\cos 60^\circ &

答案：B

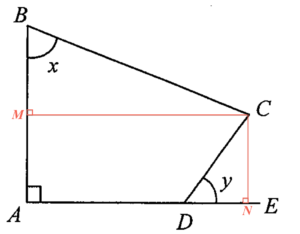
於 $AB$ 上加點 $M$ 使得 $CM\perp AB$，且於 $DE$ 上加點 $N$ 使得 $CN\per

答案：C
由於 $A+B=90^\circ$，所以 $B = 90^\circ – A$。

$\begi

答案：D
由於 $AB:BC:AC = 3:4:5$，則設 $AB=3k$、$BC= 4k$ 及 $AC = 5k$，其

答案：A
考慮 $\Delta BCE$，由於 $BC=CE$，所以 $\angle CBE = \angle CEB

答案：A
$\begin{array}{rcl}
(n-2)\times 180^\circ & =

答案：C

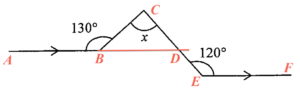
$AB$ 的延線交 $CE$ 於 $D$。由於 $ABD$ 為一直線，可得

$\begin{array}{

答案：A
在圖中加上 $A$，如下圖所示。

把該圖形旋轉至以下位置，它與原來的圖形完全地重合一次。

再把該圖

答案：D
留意點 $A$ 與直線 $x=1$ 的距離為 $4$，也留意物件與對稱軸的距離等於反射的像與對稱軸的距

答案：B
設 $(x,y)$ 為 $P$ 的坐標。

$\begin{array}{rcl}
AP & = &#

答案：A
留意 $L$ 的斜率

$\begin{array}{cl}
= & \tan(180^\cir

答案：D
基於斜截式，$L_1$ 的斜率與 $y$ 截距分別為 $a$ 和 $b$；$L_2$ 的斜率與 $y$ 截距分

答案：C
所求的概率

$\begin{array}{cl}
= & \dfrac{2}{3}\tim

答案：C
設 $x\text{ cm}$ 為男生的平均身高。由此，可得

$\begin{array}{rcl}

答案：C
I 為錯誤。分佈域

$\begin{array}{cl}
= & 36 – 4 \\
=

答案：D
留意 $y=g(x) = \frac{1}{3} f(x)$。所以，$g(x)$ 為把 $f(x)$ 沿 $

答案：C
$\begin{array}{cl}
& 1234^{3235} \\
\approx &#

答案：D

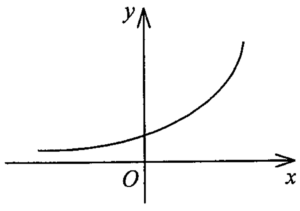
設 $f(x) = 3^x$。上圖為 $y=f(x)=3^x$ 的圖像。

$\begin{array}{

答案：D
$\begin{array}{cl}
& 16^{12} + 14 \\
= & 1 \t