香港中學會考 - 2010

答案：C
設 $a$ 及 $r$ 分別為該等比數列的首項及公比。則可得

$\left\{ \begin{array

答案：B

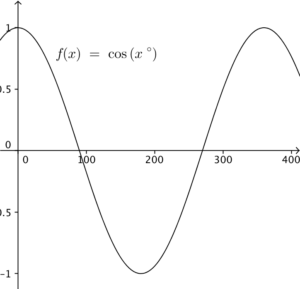
透過比較 $y=\cos x^\circ$ 的圖像，題目的圖像沿 $x$ 軸縮小至 $\frac{1}{

答案：B
$\begin{array}{cl}
& \cos^2 1^\circ + \cos^2 2^

答案：D
設 $AB=BC=AC=2x$。由於 $AB=BC=AC$，$\Delta ABC$ 為一等邊三角形

答案：D

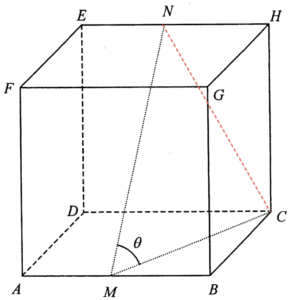
連結 $NC$。設 $2x$ 為該立方體的邊長，則 $MB=x$。利用畢氏定理於 $\Delta MBC

答案：B
標示 $O$ 為圓 $ABCD$ 的圓心，及 $Z$ 為 $BC$ 的中點。由此，$OZ \perp BC$。參

答案：C
由於 $XY$ 及 $XZ$ 分別為圓 $ABCD$ 於 $A$ 及 $B$ 的切線，則 $XA=XB$。所以，可

答案：A
考慮 $A$ 的坐標。把 $y=0$ 代入該方程，可得

$\begin{array}{rcl}
x^2 +

答案：D

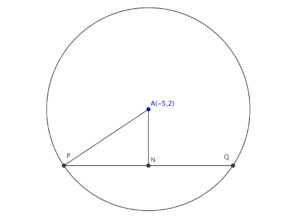
標示 $A$ 為所求的圓的圓心，及 $N$ 為 $PQ$ 的中點。所以，$\angle ANP = 90^\c

答案：A
所求的概率

$\begin{array}{cl}
= & (1-0.55)\times 0.

答案：B
A 可能錯誤。因為我們並不知道偉健和麗芳的實際支出。圓形圖的大小並不表示支出的多少。

B 必為正確