香港中學文憑-數學 - 2018 - 卷二 -

答案：B
考慮 $\Delta BDE$。

$\begin{array}{rcll}
BD & = �

答案：B
連結 $AC$ 及 $AD$。

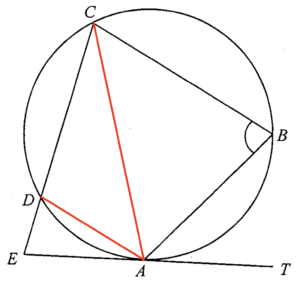
考慮 $\Delta ABC$。

$\begin{array}{rcll}

答案：(a) $25^\circ$ (b) 不是

1. 考慮四邊形 $OAED$，可得

   $\begin{array}{

答案：B
在 $\Delta OBD$ 及 $\Delta OAC$ 中，

$\begin{array}{rcll}

答案：B
考慮圓內接四邊形 $ACDE$。

$\begin{array}{rcll}
\angle DAE &#

答案：(b) (i) $1547\pi\text{ cm}$ (ii) 同意

1. 在 $\Delta UTV$ 及 $\De

答案：C
連結 $AC$ 及 $AD$。

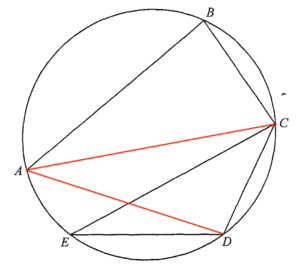
考慮 $\Delta ABC$。由於 $\angle ABC = 90^\cir

答案：A
在圓 $CDE$ 加點 $F$。連結 $DF$ 及 $EF$。

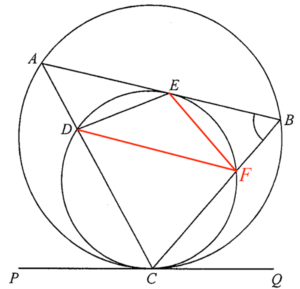
考慮 $\Delta CDF$。

$\begin

答案：A

$\begin{array}{rcll}
\angle ACD & = & 180^

答案：D

連結 $AD$。

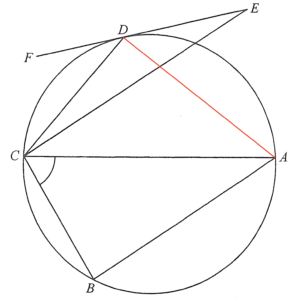
在 $\Delta CDE$ 中，

$\begin{array}{rcll}
\angl

答案：B

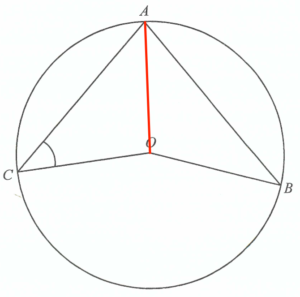
連結 $OA$。

$\begin{array}{rcll}
\angle CAB & = �

答案：C

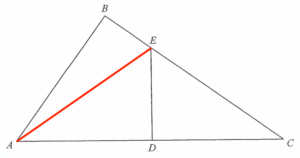
連結 $AE$。由於 $\angle ABE = 90^\circ$ 及 $ABED$ 為圓內接四邊形，則 $

答案：D

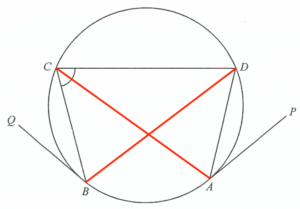
連結 $AC$ 及 $BD$。

$\begin{array}{rcll}
\angle BDC &

答案：$\angle RQS=27^\circ$, $\angle PQS=63^\circ$

在 $\Del

答案：B

設 $\angle TSU =x$。在 $\Delta STU$ 中，可得

$\begin{array}{

答案：C

連結 $P$ 及 $R$。

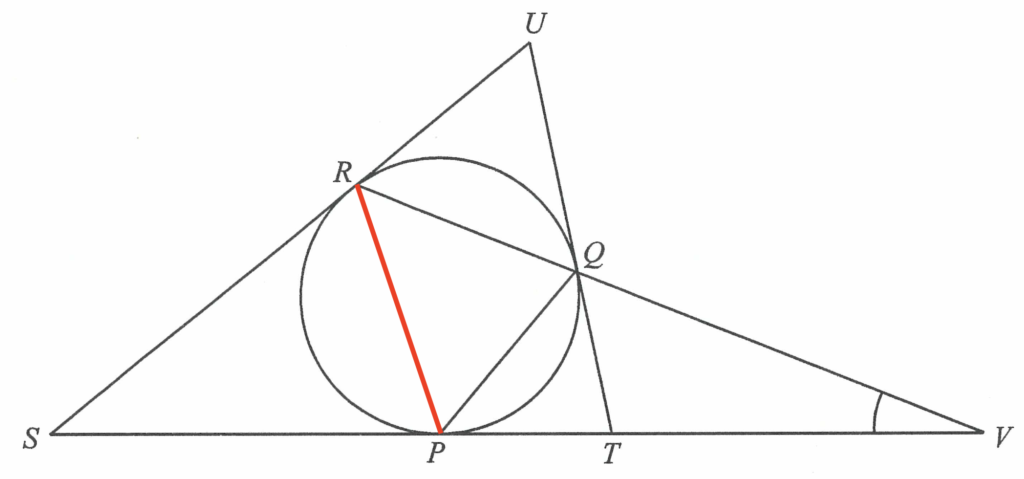
由於 $SU$ 及 $ST$ 分別為圓於 $R$ 及 $P$ 的切線，可得

$\begin