香港中學文憑-數學 - 2020 - 卷一 -

答案：(a) $700\pi\text{ cm}^3$ (b) $195\pi\text{ cm}^2$

1. 設 $r

答案：D
設 $r$ 及 $\theta$ 分別為該扇形的半徑及圓心角。

原來的弧長

$\begin{array}

答案：B
考慮該直立圓柱體的體積，可得

$\begin{array}{rcl}
\pi \times (5a)

答案：C
留意 $\Delta OPU \sim \Delta OQT$。由此，可得

$\begin{array}

答案：B
連結 $DG$。

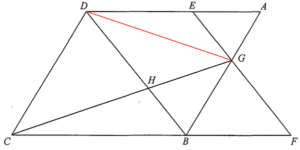
考慮 $\Delta AEG$ 及 $\Delta DEG$。若分別以 $AE$ 及 $DE$

答案：(a) $10\text{ cm}$ (b) 不相似 (c) 同意

1. 設 $r\text{ cm}$ 為 $Y$ 的底半

答案：C

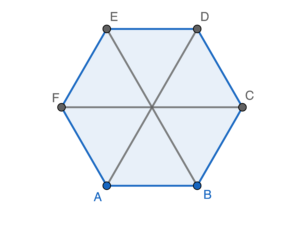
留意正 $6$ 邊形可分割為 $6$ 個等邊三角形，每邊長 $8\text{ cm}$。

底面面積

$\be

答案：A

設 $r_1 \text{ cm}$ 及 $r_2 \text{ cm}$ 分別為該兩個半球體的半徑，其中 $

答案：B

I 為正確。設 $r\text{ cm}$ 為扇形 $OAB$ 的半徑。

$\begin{array}{r

答案：C

由於 $\Delta EBF \sim \Delta DAE$，可得

$\begin{array}{rc

答案：(a) $288\pi\text{ cm}^3$ (b) 不正確

1. 由於所有球體皆相似，可得

   $\begin

答案：A

設 $r\text{ cm}$ 為該半球體的半徑。則該圓柱體的底半徑及高分別為 $r\text{ cm

答案：B

連結 $PN$。

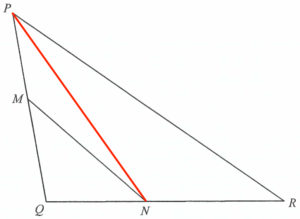
設 $x\text{ cm}^2$ 為 $\Delta MNQ$ 的面積。由於 $\Delt

答案：C

由於 $ABCD$ 為一長方形，可得

$\begin{array}{rcl}
AB & = &#

答案：(a) $48\text{ cm}$ (b) (i) $3087\pi\text{ cm}^3$ (ii) $

答案：A

設 $r\text{ cm}$ 及 $h\text{ cm}$ 分別為該直立圓柱體的底半徑及高。

由於該立

答案：D

將大圓的圓心記為 $O$。

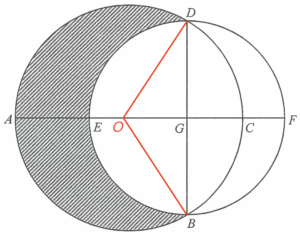
由於 $AC$ 為大圓的一直徑，可得

$\begin{array}{rcl

答案：B

連結 $R$ 及 $X$。設 $PX:XQ =r:1$，其中 $r0$。

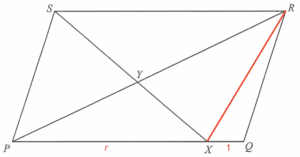
由於 $\Delta PQR$ 及 $\