2011-II-37
答案：D
考慮最基礎的情況 $y=f(x+h)+k$。
… Read 考慮最基礎的情況 $y=f(x+h)+k$。
對於 $k$ 為正數，$y=f(x)$ 向上平移 $k$ 單
香港中學會考 - 2011 - 卷二 -
2011-II-46
答案：D
參考 $y=\cos x^\circ$ 的圖像，題目中的圖像是把 $y=\cos x^\circ$ 的圖
… Read 參考 $y=\cos x^\circ$ 的圖像，題目中的圖像是把 $y=\cos x^\circ$ 的圖
2011SP-II-25
答案：A
右方的六邊形以兩個六邊形的接觸點為旋轉中心，逆時針旋轉 $90^\circ$。或者，左方的六邊
… Read 右方的六邊形以兩個六邊形的接觸點為旋轉中心，逆時針旋轉 $90^\circ$。或者，左方的六邊
2011SP-II-37
答案：C
考慮一般情況 $g(x)=f(x+h)+k$。
… Read 考慮一般情況 $g(x)=f(x+h)+k$。
若 $h$ 為正數，則函數 $f(x)$ 會向左平移 $h
2011SP-II-42
答案：B
考慮函數 $y=a\cos(x^\circ+b)$。
… Read 考慮函數 $y=a\cos(x^\circ+b)$。
$a$ 為把該函數沿 $y$ 軸放大的放大倍數。
2012-II-34
答案：C
A 不一定正確。函數 $f(x)=\dfrac{1}{2}(x-3)^2-4$ 的圖像的頂點的坐標
… Read A 不一定正確。函數 $f(x)=\dfrac{1}{2}(x-3)^2-4$ 的圖像的頂點的坐標
2012-II-38
答案：C
考慮函數 $y=f(x+h)+k$。
… Read 考慮函數 $y=f(x+h)+k$。
若 $h$ 為正數，則該函數的圖像向左平移 $h$ 單位。若 $h$
2012-II-39
答案：D
考慮函數 $y=a\cos(hx)+k$。
… Read 考慮函數 $y=a\cos(hx)+k$。
若 $k$ 為正數，該函數的圖像向上平移 $k$ 單位。若 $
2012PP-II-24
答案：D
I 具有旋轉對稱及反射對稱性質。其旋轉中心為兩條對角線的交點，且它是 $2$ 重旋轉對稱圖形。它也
… Read I 具有旋轉對稱及反射對稱性質。其旋轉中心為兩條對角線的交點，且它是 $2$ 重旋轉對稱圖形。它也
2012PP-II-31
答案：D
$g(x)=2f(x)$ 表示把 $f(x)$ 沿 $y$ 軸放大 $2$ 倍，其中 $x$ 截距不變及 $y$
… Read $g(x)=2f(x)$ 表示把 $f(x)$ 沿 $y$ 軸放大 $2$ 倍，其中 $x$ 截距不變及 $y$
2012PP-II-38
答案：C
考慮 $y=a\sin(x^\circ+\theta)$。
… Read 考慮 $y=a\sin(x^\circ+\theta)$。
若 $\theta$ 為正數，該圖像會向
2013-II-15
答案：B
該圖形四條反射對稱軸為
… Read 該圖形四條反射對稱軸為
2013-II-39
答案：A
考慮 $y=\tan x^\circ$ 的圖像。
… Read 考慮 $y=\tan x^\circ$ 的圖像。
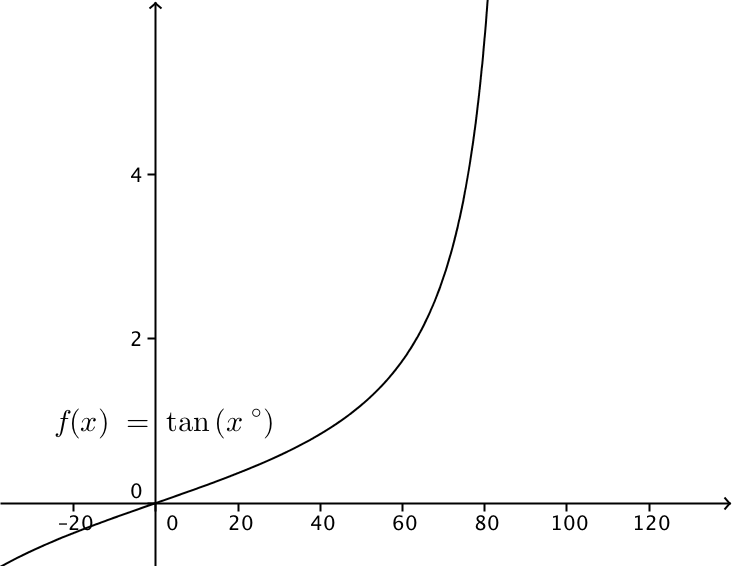
透過比較 $y=\tan x^\circ$ 及 $y=h+
2014-II-38
答案：A
留意 $y=1-f(x)$ 表示把 $y=f(x)$ 沿 $x$ 軸反射，之後再向上平移 $1$ 單位。所以
… Read 留意 $y=1-f(x)$ 表示把 $y=f(x)$ 沿 $x$ 軸反射，之後再向上平移 $1$ 單位。所以
2015-II-39
答案：D
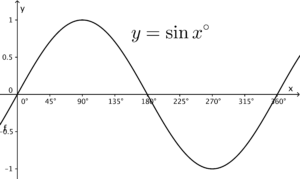
… Read 透過比較 $y=\sin x^\circ$ 與 $y=\sin(kx^\circ + \theta)$ 的
2016-II-23
答案：A
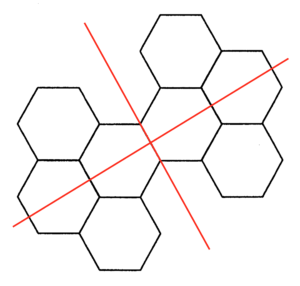
… Read 根據上圖，該圖形有 $2$ 條反射對稱軸。
2016-II-37
答案：A
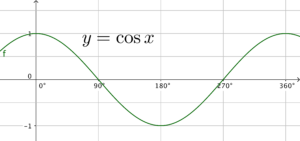
… Read 透過比較 $y=\cos x$ 的圖像，可發現 $y=\cos x$ 的圖像被沿 $y$ 軸放大至原來的 $2
2017-II-31
答案：D
留意 $g(x) = f\left(\dfrac{x}{2}\right)$ 表示 $f(x)$ 沿 $x
… Read 留意 $g(x) = f\left(\dfrac{x}{2}\right)$ 表示 $f(x)$ 沿 $x
2018-II-23
答案：B
設旋轉中心為 $O$。另外，設圖中的一點為 $A$。若把該圖像繞 $O$ 順時針旋轉 $360^\ci
… Read 設旋轉中心為 $O$。另外，設圖中的一點為 $A$。若把該圖像繞 $O$ 順時針旋轉 $360^\ci