香港中學會考 - 2006 - 卷一 -

答案：$\angle ABE=70^\circ$, $\angle BCD=40^\circ$
因為 $BC/

答案：D
在 $\Delta ABE$ 和 $\Delta ACD$ 中，

$\begin{array}{ll}
\a

答案：D
I 必為正確。留意 $\Delta ABC$ 為一等腰三角形且 $AD\perp BC$。所以，$D$ 為

答案：$x=70^\circ$, $y=20^\circ$, $z=20^\circ$
由於 $DEF$ 為一

答案：D
留意多邊形的外角和為 $360^\circ$，且 $n$ 邊形的內角和為 $(n-2)180^\ci

答案：B
加直線 $FX$ 使得 $AB//FX//CD$。由於 $AY$ 及 $CY$ 分別為 $\angle BAX

答案：C
$\Delta ABC$ 的形心必在 $\Delta ABC$ 之內。下圖顯示一鈍角三角形的形心。

$\

答案：$x=33^\circ$, $y=76^\circ$, $z=28^\circ$
由於 $AB//CD

答案：B

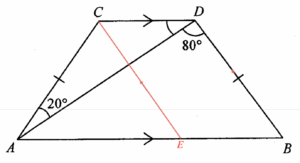
設 $\angle ADC = y$。在 $AB$ 上加點 $E$ 使得 $EC//BD$。留意 $CEBD$ 為

答案：D

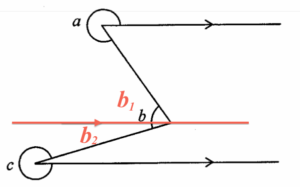
加入一水平線，該線把 $b$ 分為 $b_1$ 及 $b_2$ 兩角，參考上圖。利用平行線的性質，可得 $

答案：(b) (ii) $\Delta CBA$, $\Delta CEF$

1. 在 $\Delta ACD$ 中，

   $\b

答案：A
考慮 $\Delta BCE$，由於 $BC=CE$，所以 $\angle CBE = \angle CEB

答案：A
$\begin{array}{rcl}
(n-2)\times 180^\circ & =

答案：C

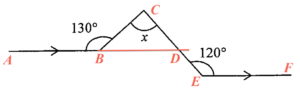
$AB$ 的延線交 $CE$ 於 $D$。由於 $ABD$ 為一直線，可得

$\begin{array}{

答案：(a) $126^\circ$

答案：A
I 必為正確。立方體的 $9$ 個反射平面如下：

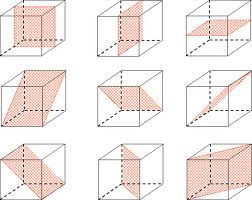
II 必為正確。立方體所有旋轉對稱軸的交點如下：

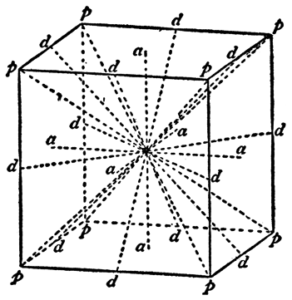
II

答案：A
$\begin{array}{rcl}
\angle ACD & = & 180^\

答案：C
正 24 邊形的內角

$\begin{array}{cl}
= & \dfrac{1}{24}

答案：(b) $42^\circ$

1. 在 $\Delta ABD$ 及 $\Delta ACD$ 中，

   $\becaus

答案：(c) $10$

1. 在 $\Delta ABP$ 及 $\Delta PCD$ 中，

   $\begin{array}